Modernizing Intro to Statistics with infer: Part 1 T-test
By Zhaoshan 'Joshua' Duan in statistics R tidyverse infer
February 24, 2022
Introduction
In this blog series, I wish to showcase the benefits of incorporating the
infer package in “Intro to Statistics” courses from a student’s perspective. The infer package provides a suite of tidyverse-friendly functions to perform statistical inference through a unified workflow framework.
Throughout the series, I plan to compare this framework with the traditional way of conducting statistical inference on some of the most common statistical topics covered in introductory statistics courses. My goal is to demonstrate how the infer framework could provide additional workflow explainability and procedural clarity in statistical inference. Such framework could potentially enhance long-term understanding of the traditional theory-based approach of statistical testing.
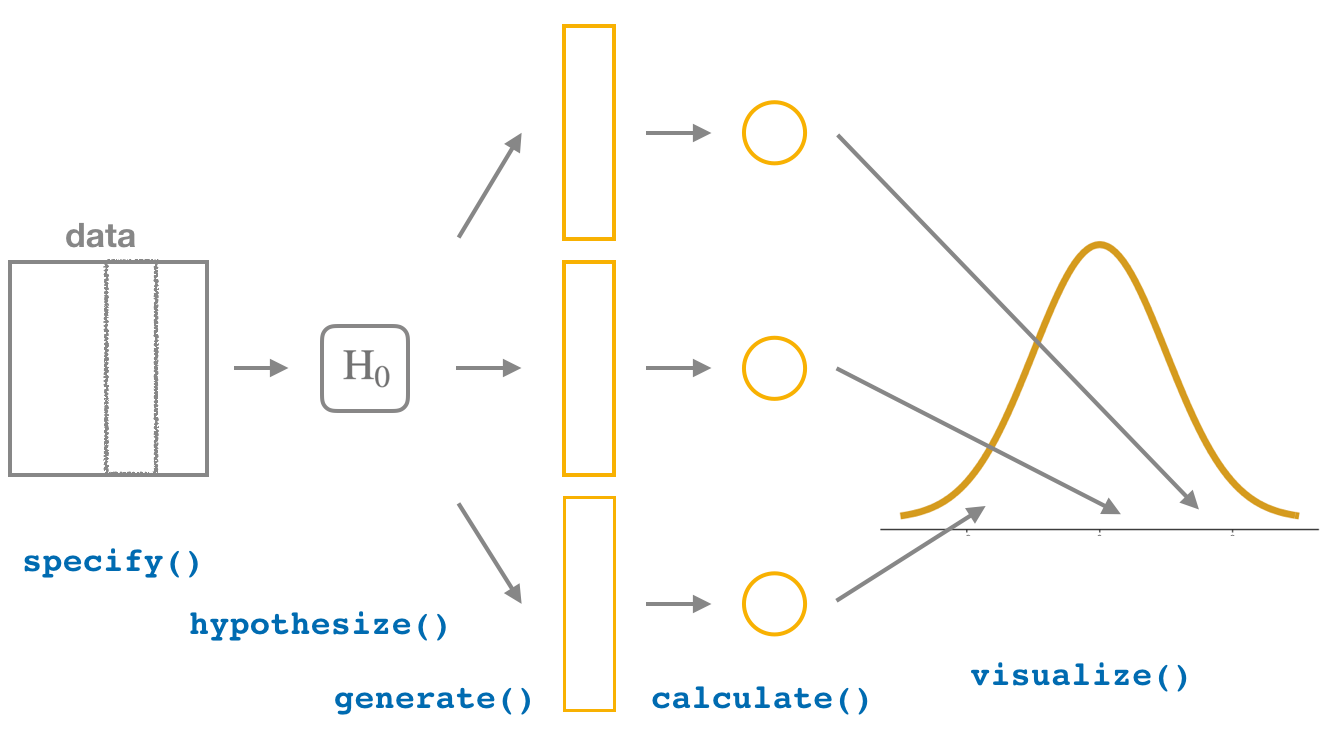
In the first blog, I focus on conducting Unpaired Two-sample \(t\)-test using the ncbirths dataset from
OpenIntro Statistics. Last Updated: March 07, 2022
Packages used
library(tidyverse)
library(infer)
library(rstatix)
library(openintro)
library(kableExtra)
Data
In this post, I make use of the ncbirths dataset from the openintro package. The ncbirths dataset records 1000 cases of North Carolina births in 2004, and has been of interest to medical researchers to study the relation between habits and practices of expectant mothers and the birth of their children. See ?ncbirth for more information about the dataset. The dataset looks like this:
ncbirths %>%
head() %>%
kbl(caption = "Recorded Births of North Carolina in 2004") %>%
kable_classic("striped",full_width = F, html_font = "Cambria")
| fage | mage | mature | weeks | premie | visits | marital | gained | weight | lowbirthweight | gender | habit | whitemom |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NA | 13 | younger mom | 39 | full term | 10 | not married | 38 | 7.63 | not low | male | nonsmoker | not white |
| NA | 14 | younger mom | 42 | full term | 15 | not married | 20 | 7.88 | not low | male | nonsmoker | not white |
| 19 | 15 | younger mom | 37 | full term | 11 | not married | 38 | 6.63 | not low | female | nonsmoker | white |
| 21 | 15 | younger mom | 41 | full term | 6 | not married | 34 | 8.00 | not low | male | nonsmoker | white |
| NA | 15 | younger mom | 39 | full term | 9 | not married | 27 | 6.38 | not low | female | nonsmoker | not white |
| NA | 15 | younger mom | 38 | full term | 19 | not married | 22 | 5.38 | low | male | nonsmoker | not white |
ncbirths %>%
select(habit, weight) %>%
ggplot(aes(x = habit, y = weight, color=habit)) +
geom_boxplot()+
labs(x = "Smoking status of mother", y = "Birth weight of baby (in lbs)") +
scale_x_discrete(labels = c("Nonsmoker", "Smoker"))

From the box plot above, we see that the median weights of the two groups are around 7 lbs, and that babies from mothers that smoke seem to weigh slightly less than babies from mothers that do not smoke. Let’s quantify the difference:
ncbirths %>%
select(habit, weight) %>%
group_by(habit) %>%
summarize(mean = mean(weight), n=n())
## # A tibble: 3 x 3
## habit mean n
## <fct> <dbl> <int>
## 1 nonsmoker 7.14 873
## 2 smoker 6.83 126
## 3 <NA> 3.63 1
The numerical output aligns with our box plot observation. Next, because our research question is to examine whether or not the difference in average weights is significant and the sample sizes of the two categories are different, we can conduct an unpaired two-sample \(t\)-test.
From our EDA, we also found one observation with missing values. We will remove it.
ncbirths_complete <- ncbirths %>%
select(habit, weight) %>%
drop_na()
Traditional Approach with t.test()
In the traditional approach, we pass these variables as either formula object or data arguments into t.test(), and start interpreting the results. For this example, we use Welch’s t-test since the variances of the two samples are not equal.
base_r_res <- t.test(weight ~ habit, data = ncbirths_complete, alternative="two.sided")
base_r_res
##
## Welch Two Sample t-test
##
## data: weight by habit
## t = 2.359, df = 171.32, p-value = 0.01945
## alternative hypothesis: true difference in means between group nonsmoker and group smoker is not equal to 0
## 95 percent confidence interval:
## 0.05151165 0.57957328
## sample estimates:
## mean in group nonsmoker mean in group smoker
## 7.144273 6.828730
This method provides quick summary results including \(t\)-statistics, \(p\)-value and 95% confidence interval. Since \(p\)-value is less than 0.05, we reject null hypothesis and conclude the difference in the average weights of the two groups is significant, and that the mother’s smoking habit has an effect on their babies' weights at birth.
However, for those who are at the beginning of their statistics education, it can look somewhat daunting without solid understandings of each of these values (maybe not as daunting as summary(lm(y ~ x))). The function also abstracts away a key aspect of hypothesis testing: the sense of workflow. While some argue that instructors can fill these gaps, I think that there exists a better tool that helps the instructors complete this picture more effectively.
Let’s see what can we do with the infer package.
Moderndized Approach with infer
The
infer package features 4 main verb functions in its statistical inference framework with emphasis on transparency in statistical inference. These functions are designed to be coherent with the tidyverse design frameworks. Let’s go through each step of the workflow.
specify()
We first specify the variables of interest. We set weight as the response variable, and habit as the explanatory variable.
ncbirths_complete %>%
specify(weight ~ habit)
## Response: weight (numeric)
## Explanatory: habit (factor)
## # A tibble: 999 x 2
## weight habit
## <dbl> <fct>
## 1 7.63 nonsmoker
## 2 7.88 nonsmoker
## 3 6.63 nonsmoker
## 4 8 nonsmoker
## 5 6.38 nonsmoker
## 6 5.38 nonsmoker
## 7 8.44 nonsmoker
## 8 4.69 nonsmoker
## 9 8.81 nonsmoker
## 10 6.94 nonsmoker
## # ... with 989 more rows
hypothesize()
Next, we construct the hypotheses. For our research question, we are examining the average weight difference between babies whose mothers do or do not smoke.
$$
\begin{aligned} H_0: \mu_{\text{nonsmoker}} - \mu_{\text{smoker}} = 0\\ H_A: \mu_{\text{nonsmoker}} - \mu_{\text{smoker}} \ne 0 \end{aligned}
$$
hypothesize() is used to declare the null hypothesis for generating the null distribution later. We pipe the previous step into hypothesize() and set null = "independence" since we are interested in studying the relationship between two variables.
ncbirths_complete %>%
specify(weight ~ habit) %>%
hypothesize(null = "independence")
## Response: weight (numeric)
## Explanatory: habit (factor)
## Null Hypothesis: independence
## # A tibble: 999 x 2
## weight habit
## <dbl> <fct>
## 1 7.63 nonsmoker
## 2 7.88 nonsmoker
## 3 6.63 nonsmoker
## 4 8 nonsmoker
## 5 6.38 nonsmoker
## 6 5.38 nonsmoker
## 7 8.44 nonsmoker
## 8 4.69 nonsmoker
## 9 8.81 nonsmoker
## 10 6.94 nonsmoker
## # ... with 989 more rows
generate()
We can now generate simulated distributions of our data from specify() assuming the null hypothesis is true. That is, under \(H_0\), the mother’s smoking habit does not have an effect on their babies' weights at birth. Using permutation, we generate 1000 replicates of the sample.
ncbirths_complete %>%
specify(weight ~ habit) %>%
hypothesize(null = "independence") %>%
generate(reps = 1000, type = "permute")
## Response: weight (numeric)
## Explanatory: habit (factor)
## Null Hypothesis: independence
## # A tibble: 999,000 x 3
## # Groups: replicate [1,000]
## weight habit replicate
## <dbl> <fct> <int>
## 1 7.31 nonsmoker 1
## 2 8.88 nonsmoker 1
## 3 7.88 nonsmoker 1
## 4 7.06 nonsmoker 1
## 5 6.25 nonsmoker 1
## 6 7.06 nonsmoker 1
## 7 8.25 nonsmoker 1
## 8 6.94 nonsmoker 1
## 9 2.69 nonsmoker 1
## 10 6.75 nonsmoker 1
## # ... with 998,990 more rows
calculate()
Next, let’s calculate the sampling distribution under null and observed statistics. Since we are conducting an Unpaired Two-sample T-test, we calculate the \(t\)-statistics by setting stat = "t".
$$ T = \frac{\overline{Y}_1 - \overline{Y}_2}{\sqrt{s^2_1/N_1 + s^2_2/N_2}} $$
Sample distribution under null, or Null Distribution:
set.seed(42)
null_dist <- ncbirths_complete %>%
specify(weight ~ habit) %>%
hypothesize(null = "independence") %>%
generate(reps = 1000, type = "permute") %>%
calculate(stat = "t", order = c("nonsmoker", "smoker"))
We calculate the observed \(t\)-statistics by omitting the hypothesize() and generate() steps:
obs_t <- ncbirths_complete %>%
specify(weight ~ habit) %>%
# hypothesize(null = "independence") %>%
# generate(reps = 1000, type = "permute") %>%
calculate(stat = "t", order = c("nonsmoker", "smoker"))
obs_t
## Response: weight (numeric)
## Explanatory: habit (factor)
## # A tibble: 1 x 1
## stat
## <dbl>
## 1 2.36
As expected, the observed statistics is the same as the statistics we got from t.test().
base_r_res$statistic
## t
## 2.359011
visualize()
Piping the previous steps into visualize(), We can visualize our null distribution. When studying \(t\)-test, we often look at the theoretic \(t\)-distribution with the degrees of freedom of the sample. In infer, we can plot both by setting method = "both" in visualize(). Because visualize() is a wrapper function of ggplot, we can customize the plot with ggplot syntax.
null_plot <- null_dist %>%
visualize(method = "both", dens_color = "blue") +
annotate(
geom="label",
x=0, y=0.15,
label="Simulated Null Distribution",
fill = "grey",
colour="black", size=3, fontface="bold") +
labs(x="t-statistics",
y="Density")
null_plot

shape_p_value() & get_p_value()
Finally, this is where infer shows great potential to add to the traditional way of hypothesis testing with base R. Using shape_p_value(), we can easily add the location of observed \(t\)-statistics obs_stat onto the null distribution to look at how likely or unlikely to observe the value.
The function also shade the areas in which data are more extreme than the observed \(t\)-statistics. Recalled that we are doing a two-sided test, we set direction = "both". And just in one line, we have visualized the \(p\)-value:
p_plot <- null_plot +
shade_p_value(obs_stat = obs_t, direction = "both")
p_plot

Let’s annotate the graph so it’s more clear.
p_plot +
annotate(
geom="label",
x=1.2, y=0.5,
label="Observed t-statistics = 2.359",
colour="red", size=4, fontface="bold") +
annotate(
geom="label",
x=3, y=0.03,
label = "p-value",
colour="#CC0000", size=4, fontface="bold") +
annotate(
geom="label",
x=-3.5, y=0.03,
label = "p-value",
colour="#CC0000", size=4, fontface="bold")

Looking at the shaded regions in the plot above, it’s quite rare to observe the \(t\)-statistics calculated from our data if null hypothesis is true. To quantify the area, we get the exact value of the \(p\)-value with get_p_value():
null_dist %>%
get_p_value(obs_stat = obs_t, direction = "both")
## # A tibble: 1 x 1
## p_value
## <dbl>
## 1 0.024
This simulated value is close to the \(p\)-value we get from t.test():
base_r_res$p.value
## [1] 0.01945056
Because the \(p\)-value is less than the our significance level \(\alpha = 0.05\), we reject the null hypothesis that and conclude the difference in the average weights of the two groups is significant. This is consistent with the t.test() result with the same significance level.
get_confidence_interval()
Let’s also look at the confidence interval of the mean difference. With infer, we can generate bootstrap distribution with small changes to our code when generating null distribution of \(t\)-statistics:
- Omit
hypothesize() - Change resampling type in
generate()to"bootstrap" - Change statistics type in
calculate()to"diff in means"
set.seed(42)
bootstrap_dist <- ncbirths_complete %>%
specify(weight ~ habit) %>%
# remove hypothesize()
# hypothesize(null = "independence") %>%
generate(reps = 1000, type = "bootstrap") %>% # change `type` to "bootstrap"
# change stat to "diff in means"
calculate(stat = "diff in means", order = c("nonsmoker", "smoker"))
From the bootstrapped sampling distribution, we can either use the percentiles to get the confidence intervals:
percentile_ci <- bootstrap_dist %>%
get_confidence_interval(level = 0.95, type = "percentile")
percentile_ci
## # A tibble: 1 x 2
## lower_ci upper_ci
## <dbl> <dbl>
## 1 0.0752 0.569
Or we can calculate it directly with observed difference in means, and standard error:
se_ci <- bootstrap_dist %>%
get_confidence_interval(level = 0.95, type = "se",
point_estimate =
ncbirths_complete %>%
specify(weight ~ habit) %>%
calculate(stat = "diff in means",
order = c("nonsmoker", "smoker")))
se_ci
## # A tibble: 1 x 2
## lower_ci upper_ci
## <dbl> <dbl>
## 1 0.0622 0.569
When we compare the two pairs of values: (0.0752, 0.5688) and (0.0622, 0.5689) with the t.test() confidence interval result, we can see that they are quite close.
base_r_res$conf.int
## [1] 0.05151165 0.57957328
## attr(,"conf.level")
## [1] 0.95
Conclusion
Clearly, the infer framework requires a lot more codes and work than t.test(). However, I think the awards greatly outweigh the additional work. By just looking at the codes, infer provides a sense of workflow that t.test() doesn’t provide. Running t.test() feels like clicking on a button to use an existing tool (or interface) to display numeric outputs, running infer feels like you are gradually building up a tool to get these results.
Such transparency in statistical inference, and explainability in workflow help the statisticians tell their data story, whether it be teaching beginners in “Intro to Statistics” courses or collaborating with those who are not well-versed in statistics in a team. t.test() gives a data summary, infer tells a data story.
t.test()gives a data summary,infertells a data story.
In the title of the blog, I used the word “modernize” because of the necessity of programming skills in the modern landscape of using statistics.
Statistics should be learned as both Math and programming. infer fits the modern workflow better because it breaks things down, and more visual, and bridges nicely into the mathematical theories behind these tests.
Coming Next …
It can be observed that infer emphasizes on data and simulation instead of probability theories and test. Coming next, I will write about infer’s greatest strength: simulation-based inference with Permutation Test!
- Posted on:
- February 24, 2022
- Length:
- 11 minute read, 2271 words
- Categories:
- statistics R tidyverse infer
- See Also: